Description :
Instrument en bois en trois morceaux, une glissière (83 cm x 1,2 cm x 0,9 cm), une équerre (de côtés 40 cm et 84 cm, section 4 cm x 0,9 cm et 1,2 cm x 0,9 cm) et une barre (102 cm de longueur), dite diagonale, munie d'une petite roue (de diamètre 1,8cm) et d'une cale en forme de demi-cercle (de diamètre 7 cm et d'épaisseur 0,9 cm). L'axe de rotation de la petite roue est perpendiculaire à la barre, fixé dans l'épaisseur de la cale de sorte que le bord "coupant" de la petite roue dépasse légèrement et marque le papier. La barre diagonale est contrainte à passer le long d'un clou fixé dans la base de l'équerre par un lien (ici en fil de pêche transparent) entourant glissière, barre et équerre qui permet uniquement glissement de la barre le long du clou, de l'équerre le long de la glissière.
Fonctionnement :
La courbe est tracée par la petite roue lorsque l'on pousse son support (en appuyant légèrement dessus) contre l'équerre, forçant le déplacement de translation de l'équerre le long de la glissière. La petite roue reste à une distance constante du clou durant le mouvement. La courbe tracée est une courbe exponentielle car elle est à sous-tangente constante.
Mode opératoire :
Grâce à une simulation Geogebra, on peut "construire" la courbe ici ou juste en voir la "construction" ici. Mais ce sont des simulations et non des constructions, le mouvement tractionnel ne pouvant être mis en œuvre réellement de cette manière (bientôt un film des constructrices en action sera disponible).
Instrument réalisé par A. Le Meur, A. Pihouet et M.Robic dans le cadre du cours de Licence de mathématiques Ouverture vers les masters en 2019-2020 à partir de la référence :
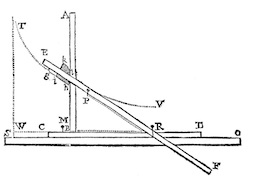
Dominique Tournès, Construction tractionnelle des équations différentielles, Blanchard, Paris, 2009, pp. 51-58, et du schéma suivant de la machine de Perks (1706) pour la quadrature de l'hyperbole.
N° PATRIMOINE : Proto006