Description :
Un support cartonné (d'épaisseur environ 5 mm), un rectangle (12 cm x 32 cm, épaisseur 0,9 cm), une glissière en bois (longueur : 80 cm, section : 3 cm x 0,9 cm), une ficelle de longueur supérieure à la hauteur du rectangle, un clou planté dans le support en un point F qui n'appartient pas à la glissière, une pointe plantée dans l'épaisseur du haut du rectangle à laquelle est accrochée une extrémité de la ficelle. Une fois le clou placé, l'autre extrémité de la ficelle est accrochée au clou. La position du clou et la longueur de la ficelle entre ses deux points d'attache déterminent la parabole que l'instrument permet de tracer. Si cette longueur est égale à la hauteur du rectangle, l'instrument peut tracer la parabole de foyer F et de directrice la glissière.
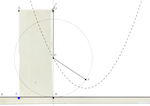
Mode opératoire :
Considérons le cas où la longueur de la ficelle est égale à la hauteur du rectangle (comme sur l'image) ; placer le rectangle contre la glissière, avec la pointe d'un stylo placée contre le rectangle, tendre la ficelle. Pour une position du rectangle sur la glissière, il n'y a qu'une position possible pour la pointe du stylo : le point marqué est à égale distance du point F et de la glissière, il appartient donc à la parabole de foyer F et de directrice la glissière. Pour tracer la demi-parabole (d'un côté du foyer) d'un seul trait continu, il suffit de faire glisser le rectangle le long de la glissière en maintenant la ficelle tendue. Pour avoir l'autre demi-parabole, il suffit de poser le rectangle de l'autre côté du foyer.
Pour voir (et manipuler) une animation Geogebra de l'instrument, cliquer ici
Pour comprendre pourquoi cette courbe est bien la courbe représentative de la fonction carré dans un bon repère ou pourquoi elle est aussi la section d'un cône de révolution par un plan parallèle à son axe de révolution, suivre ce lien.
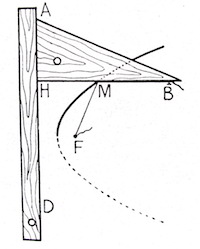
Instrument réalisé par A. Homburger et L. Weibel dans le cadre du cours de Licence de mathématiques Ouverture vers les masters en 2018-2019. La ressource étudiée était Camille Lebossé and Corentin Hémery, Géométrie, Nathan, Paris, 1961, pp. 271-373. Dans ce grand classique, on peut trouver l'image ci-contre pour le tracé continu de la parabole.
N° PATRIMOINE : proto005